Sea una función constante f(x) =k
Su gráfica es, como se sabe, una recta paralela al eje de abscisas. Puesto que para cualquier valor de la abscisa su ordenada correspondiente es, constantemente, igual a k, si a es un punto cualquiera del campo de definición de f(x),
f(a + h) - f(a) = k - k = 0, por lo que
Luego la derivada de una constante es siempre cero.
Derivada de una función identidad
La derivada de una función identidad es igual a 1
| Se suele escribir: |
|
Explicación: |
La derivada de una potencia o función potencial, es igual al exponente por la base elevada al exponente menos uno y por la derivada de la base.
Si la base es la función identidad, la derivada es igual al exponente por la base elevada al exponente menos uno.
f(x) = xk f'(x)= k · xk−1
![]()
![]()
Derivada de un producto
La derivada del producto de dos funciones es igual al primer factor por la derivada del segundo más el segundo factor por la derivada del primero.
Ejemplo:Derivada de una constante por una función:La derivada del producto de una constante por una función es igual al producto de la constante por la derivada de la función.
Ejemplo: ![]()
Derivada de un cociente
La derivada del cociente de dos funciones es igual a la derivada del numerador por el denominador menos la derivada del denominador por el numerador, divididas por el cuadrado del denominador.
Derivada de una constante partida por una función:
Ejemplos:![]()
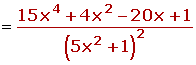















No hay comentarios:
Publicar un comentario