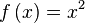DERIVADAS

7 de noviembre de 2009

¿QUÉ ES LA DERIVADA?

Geométricamente es la pendiente de la recta tangente a un punto de una curva. Y en una función mide el coeficiente de variación de dicha función. Es decir, provee una formulación matemática de la noción del coeficiente de cambio. El coeficiente de cambio indica lo rápido que crece (o decrece) una función en un punto (razón de cambio promedio) respecto del eje "x" de un plano cartesiano de dos dimensiones. Por ejemplo si tomamos la velocidad de algo, su coeficiente es la aceleración, la cual mide cuánto cambia la velocidad en un tiempo dado.

La función derivada se puede calcular sin dibujar la curva de f. En efecto, gracias a una propiedad geométrica de la tangente, se tiene la fórmula:

$f^\prime(x) = \lim_{h \to 0} \frac {f(x+h) - f(x)} {h}$

Por ejemplo, sea

$f\left(x\right) = x^2$

entonces:

$\begin{array}{rcl} f^\prime(x) &=& \displaystyle \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}\\ &=& \displaystyle \lim_{h \to 0} \frac{(x+h)^2 -x^2}{h}\\ &=& \displaystyle \lim_{h \to 0} \frac{x^2 + 2xh + h^2 - x^2}{h}\\ &=& \displaystyle \lim_{h \to 0} \frac{2xh + h^2}{h}\\ &=& \displaystyle \lim_{h \to 0} (2x + h)\\ &=& 2x \end{array}$

Ejemplo

Calcular la derivada de la función f(x) = 3x² en el punto x = 2.

NOTACIONES DE DERIVADA

Si f es una función, se escribe la derivada de la función f al valor ‘x’ en varios modos:

6 de noviembre de 2009

PENDIENTE DE UNA CURVA

La pendiente de una curva en un punto es la inclinacion que t

iene la recta tangente a ese punto, pero para entender este concepto, primero debemos saber que la recta tangente a una curva es aquella que solo la cota en un punto, y la obtenemos acercando uno de los puntos de una secante (recta que corta la curva en 2 puntos) hacia el otro

un ejemplo de la pendiente de una curva pude ser ubicr los puntos ( x , f

(x) ) y (x+h , f(x+h) )en la siguiente parabola y hallar la pendiente de la recta tangente.

30 de octubre de 2009

PENDIENTE DE UNA LINEA RECTA

La pendiente es el grado de inclinación de una recta con respecto a la horizontal, y la representamos con la letra “m”. Geométricamente podemos decir que es la tangente del ángulo que se forma entre la línea recta y el eje positivo de las “x”.

Para calcular la pendiente solo es necesario calcular la tangente del ángulo formado entre el eje “x” y la recta partiendo de la horizontal y en sentido anti horario

ejemplo:

en este caso el angulo de inclinación es α, entonces

m= tan α

y si α= 45°

m= tan 45°

m= 1.61

Sin embargo no siempre nos dan el ángulo de inclinación de la recta, sino que nos dan dos puntos con coordenadas (x, y). En estos casos utilizamos la formula

Ejemplo: para calcular la pendiente de una recta que pasa por los puntos

(2, 2) y (3, 5)lo único que hay que hacer es reemplazar